En fin oppsummering av The imitation game:

http://www.slate.com/blogs/browbeat/2014/12/03/the_imitation_game_fact_vs_fiction_how_true_the_new_movie_is_to_alan_turing.html

Trailer:

The testing camera

Oppjazzet Pytagoras

Pytagoreikerne var opptatt av musikk, hadde hemmelige symboler og rare leveregler å forholde seg til. Mer eller mindre en slags kult som diskuterte farlige ideer verden ikke måtte få vite om. Så hvorfor ikke kombinere et bevis for Pytagorassetningen med litt klassisk musikk? :) (via Matematikkdidaktikk-gruppa på facebook)

Nettfunn 14.12

An impossible bet

Nettfunn 7.12.14

Matematikken som trengs (eller ikke trengs) for å pakke inn julegaver:
http://mentalfloss.com/article/60493/how-wrap-present-mathematical-precision-and-waste-less-paper

Litt grums om nasjonale prøver må vi koste på oss.
http://www.dagbladet.no/2014/12/05/kultur/meninger/debatt/kronikk/skolepolitikk/36572426/

Simpson vs. Fermat
https://www.youtube.com/watch?v=ReOQ300AcSU

Ja, hva er et bevis egentlig?
http://profkeithdevlin.org/2014/11/24/what-is-a-proof-really/

En gjeng matematikere finner de gladeste ordene i språket
http://mentalfloss.com/article/31974/25-happiest-words-english

Play Osmo ser ut som et ganske morsomt tillegg til podens iPad!
https://www.playosmo.com/home.html?utm_expid=85506917-16.AVN-cYFeT2Ky6YpwrR7puw.1

Notion in motion, om læreres digitale kompetanse
http://www.idunn.no/dk/2014/04/notion_in_motion_teachersdigital_competence_#.VIAIjM2h-30.facebook

Nettfunn sist uke

Vanskelig å sammenlikne undervisningsresultater forskningsmessig
http://www.vg.no/forbruker/teknologi/skole-og-utdanning/lite-forskning-paa-laeringsutbyttet/a/23332904/

MOOCs fra store universiteter:
http://www.openculture.com/free_certificate_courses

Matematikksenterets blogg om Hunger Games
http://matematikksenteret.no/content/4639/The-Hunger-Games:-Mockingjay-Changes

Nettfunn sist uke

To sider av USAs utdanningsreform:
http://www.salon.com/2014/08/09/secrets_of_amazing_teachers_what_both_sides_of_the_education_reform_debate_get_wrong_about_autonomy_and_accountability/

Sorteringsalgoritme. Ganske stilig å se på.
http://9gag.com/gag/aPyoG4P

Neida, vi har ikke glemt at det er artig med papirfly!
http://www.sciencedump.com/content/tutorial-paper-airplane-actually-flies

Fibonacci
http://www.sciencedump.com/content/magic-fibonacci-numbers

Ikke kast TI-83'n - den kan spille spill!
http://nerdapproved.com/gaming/you-can-play-super-smash-bros-on-a-ti-83-or-ti-84-calculator/

Nettfunn sist uke

En flott tegneserie, "They used science". Sjekk også ut annet fra http://zenpencils.com/!
http://www.sciencedump.com/content/they-used-science-comic

Arne Kåre Topphol er førsteamanuensis ved Høgskulen i Volda (og ikke Volga, som det står i artikkelen), men han har lansert kritikk mot Überpedagog Hatties bruk av statistikk. Hattie på sin side svarer at han er klar over at halvparten av statistikken hans ikke holder. Underlig å fortsatt høste fruktene av slik massiv oppstandelse som han har forårsaket, uten å kommentere dette, er det ikke? Det gjør det iallfall ikke enklere å ta resultatene hans for god fisk.
http://ollieorange2.wordpress.com/2014/08/25/people-who-think-probabilities-can-be-negative-shouldnt-write-books-on-statistics/

En app som ser veldig handy ut! Ta bilde av ei eller flere sider fra ei bok og få resultatet lagt i dropboxen din som pdf.
http://mathandmultimedia.com/2014/11/08/genius-scan/
Android app her: https://play.google.com/store/apps/details?id=com.thegrizzlylabs.geniusscan.free&hl=en

Forklaringen på matematikkvitser...
http://www.sciencedump.com/content/math-jokes-explained

Derfor bruker vi X
http://www.gizmodo.com.au/2014/11/why-we-use-x-as-the-unknown-in-math/




Why is Math Different Now from raj shah on Vimeo.

Link til side i pdf

Relativt stor oppdagelse for meg, og noe som sikkert folk flest har visst i tiår. Er inne i en prosess med å samle sammen artikler og ting man har skrevet for å en dag kunne søke om opprykk. Da er det behov for å lenke til skribleriene sine. Problemet er når disse står langt bak i et svææært pdf-dokument. Så litt ut av det blå dukket løsningen opp.
Legg til en #page=69 (eller et annet sidetall) og leseren fraktes direkte til angitt side når man trykker på lenka! Smart :)
http://www.caspar.no/tangenten/2005/t2005-3.pdf#page=69 

Kolleger på twitter

Lærerutdanningen på HiST har flere kvitrere rundt omkring i korridorene. Her er de jeg vet om i farten!

Ivar Sørensen
https://twitter.com/ivarsorensen

Marion G. Stavsøien
https://twitter.com/MarionStavsoien

Harald Morten Iversen
https://twitter.com/haraldmi

Torkel Haugan Hansen
https://twitter.com/torkelhh

Svein Arne Sikko
https://twitter.com/SveinArneSikko

Stian Hårstad
https://twitter.com/avlyd

Calle Dons
https://twitter.com/calledon

Jan Frode Haugseth
https://twitter.com/jafro77

Siri-Malèn Høynes
https://twitter.com/sirimalen

Ruth Grüthers
https://twitter.com/rutgru

Hvem har jeg ikke fått med meg, tro?

Her er flere av dem samlet i ei liste: https://twitter.com/oisteing/lists/tweets-fra-hist

Funnet på nettet sist uke!

Matematisk modell for hipsteres klesvalg (!)
http://mic.com/articles/103172/the-scientific-reason-all-hipsters-look-the-same

Å måle radianer
http://imgur.com/gallery/lJPJsrA

Samling med 12 litt problematiske sammenhenger i matematikk
http://www.businessinsider.com/the-most-controversial-math-problems-2013-3

The random mathematical ponderations of a math geek
http://mathynick.com/

Calculus Rhapsody
https://www.youtube.com/watch?v=uqwC41RDPyg

Litt mer Desmos

Selv om GeoGebra nok er programmet jeg tyr til for alt i geometri og algebra, så har jeg blitt litt misfornøyd med at det som var et program hvem som helst kom i gang med nå blir mer og mer komplekst. Jeg vet mange foretrakk GeoGebra foran TI-nspire nettopp på grunn av dette. Kanskje kan det være greit å se at det fins alternativer, iallfall om det bare skal noe småtteri til. Ei nettside som har høy popularitet i USA er Desmos, og selv om denne sida i bunn og grunn er en graftegner har den noen egenskaper som er verdt å merke seg. Blant annet hvordan man lager glidere for parametre. Se her:

Desmos gir deg et noenlunde standard grafvindu som du kan gjøre vanlige ting med (skalere, flytte osv).

På menyen øverst til venstre kan du legge til ting, f.eks. funksjoner (som du skal tegne grafen til) eller bilder og tekst. Bilder og tekst kan være nyttig om du skal lage grafen PÅ et bilde, for eksempel.

La oss sette inn det vanlige uttrykket for en lineær funksjon. Når vi skriver y=ax+b så ser vi at det dukker opp noen knapper under mens vi skriver:

Det betyr at vi kan lage glidere for disse parametrene bare ved å klikke på knappene det står a og b på. (Eller "all" for å lage glidere for alt på en gang.)

Grafen til funksjonen tegnes med en gang - glidebryterne settes inn automatisk. Så lett er det å lage et interaktivt arbeidsark til å undersøke stigningstall og konstantledd med.
Du kan også klikke på tannhjulet til høyre for å se at du kan velge intervall på gliderne og farge på grafen.

GeoGebra var kjempelett på slike ting før (og er det fortsatt), men lurer på om ikke dette var enda enklere! 

Geobrett

 Du kan lese mer om Picks teorem på f.eks. denne bloggposten: https://reflectionsinthewhy.wordpress.com/tag/geoboards/ 

Et konkretiseringhjelpemiddel vi ofte bruker i matematikk er geobrettet, også kalt pluggbrett. I sin konkrete, fysiske form er dette typisk et kvadrat med spiker i som på bildet (Wikipedia). Vi har plastikkvarianter av disse i bøtter og spann på lærerutdanningen.

Matematikksenteret skriver om Geobrett flere steder. Her kan du finne oppgaver (8 sider pdf) og en idebok (pdf 56 sider) (Sistnevnte er tydeligvis norsk oversettelse av boka Just for Geoboards). Vil du ikke lage brettene selv kan du kjøpe de f.eks. her.

Hva slags oppgaver kan disse brettene brukes til? Vel, det er nok bare fantasien som setter grenser her. Typiske oppgaver er "Hvor mange kvadrater kan du lage på Geobrettet? Det høres jo lett ut, man har et stort kvadrat (hele brettet, sidekanten har da lengde fire, hvis vi setter avstanden mellom spiker til å være 1), seksten små og så er det en liten tellejobb for å finne kvadratene som har sidekant på to og de som har sidekant tre. Men ser vi på bildet øverst så ser vi at det også fins kvadrater som står på skrå. Eller er det kvadrater? Hvordan kan vi finne ut sidelengdene her i så fall? Og hvordan vet vi at det er rett vinkler i hjørnene?

Det er også andre muligheter med todimensjonal geometri. Kan du f.eks. finne et heksagon uten parallelle sider? Kan du finne en likebeint og rettvinklet trekant? Eller en spiss, likebeint trekant?
Symmetrier er at annet tema man kan eksperimentere med. Kan vi lage figurer med en symmetriakse/speilakse? Hva med to akser? Eller tre?
Et naturlig tema er areal av figurer og her fins det mange muligheter. Lag en hvilken som helst figur og finn arealet av den. Kan vi finne arealet på flere måter? Kan du lage figurer med likt areal, men forskjellig lengde på omkretsen? Eller motsatt, lik omkrets og forskjellig areal?

Det er kanskje ikke like naturlig å tenke på brøk som tema på geobrettet. Kanskje kan elevene prøve å illustrere 1/2 eller 3/4 på forskjellige måter? Hva med 3/5?
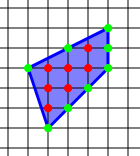Litt mer avanserte muligheter fins også. Et kjent problem/resultat er Picks teorem. Hvis vi lager et polygon på geobrettet så vil noen spiker være hjørner, mens det kan være andre spiker både inni figuren og på kanten av figuren. Vi kan da bruke formelen til Pick til å regne ut arealet av figuren når vi vet antall spiker inni figuren (i) og antall spiker langs kanten (og i hjørnene) av figuren (b), Da blir arealet \( A=i+\frac{b}{2}-1\). På bildet (fra wikipedia) har vi 7 punkter inni og 8 på randen, så arealet blir \(A=7+\frac{8}{2}-1=10\).


Det kan også være greit å ha en interaktiv variant av geobrettet, til bruk på SMARTboard eller nettbrett. Den interaktive varianten av geobrettet, som du så på bloggen til Reflections in the why, kan du finne på
http://www.mathlearningcenter.org/web-apps/geoboard/

Funnet på nettet siste uke

Hva kan du bli når du studerer realfag, da tru?
http://hvakanjegblimedrealfag.no/

Leter man på nettet etter algoritmer kan man finne en hel skokk av morsomme, nyttige og unyttige algoritmer. De fleste av dem klarer vi å gjennomskue slik at vi kan fastslå om de virker hver gang eller ikke. Felles for mange er at de er effektive i gitte situasjoner og dårlige andre ganger. Men siden det er tungvint å huske hvilke situasjoner den og den algoritmen passer best i, så har vi holdt oss til å lære få algoritmer - som fungerer så bra som mulig. I senere tid har fokuset vært mer på å unngå algoritmene, men fokusere på forståelsen bak. Det er greit å kunne noen algoritmer for å håndtere hverdagssituasjoner, men i realiteten har vel disse standardalgoritmene hatt et mye større fokus enn hva som er nødvendig. Her er en algoritme som du kan bruke når du skal undersøke subtraksjon sammen med elevene dine.
http://matematikksenteret.no/content/4594/Kan-du-forklare-denne-nydelige-subtraksjonsalgoritmen

En ny type matematisk legeme er visstnok funnet? Igjen?
http://www.iflscience.com/editors-blog/after-400-years-mathematicians-find-new-class-solid-shapes

Er matematikk oppdaget eller oppfunnet? (Ja, som om vi kan svare på det...)
http://ed.ted.com/lessons/is-math-discovered-or-invented-jeff-dekofsky

Ti prinsipper for multimedialæring:
http://ericsnewblog.blogspot.no/

Fra Better explained finner vi en, om ikke ny så iallfall annerledes, forklaring av definisjonen av sinus.
http://betterexplained.com/articles/law-of-sines/

Litt om Abel dukket opp på plusmath
http://plus.maths.org/content/stubborn-equations

Litt depressiv fysikk
http://thedoghousediaries.com/5916

Vektorsymbolet i Word

Å skrive vektorsymboler, vanligvis en eller to bokstaver med en høyrepil over, er lett ved å bruke aksent-menyen i Word. Men skal du gjøre det hundre ganger i et dokument er det en tolmodighetsprøve. Da er det greit med en lett og rask måte å gjøre det på (kan være en fordel å maksimere vinduet nedenfor):

Filmtips (tror jeg): Geometria

Likte du Pacific Rim? (Ja, det gjorde du, den inneholder tross all gigantiske og mekaniske analoge og digitale slåssmaskiner. Og øglemonstre på størrelse med et middels norsk tettsted.) Regissøren Guillermo del Toro har gjort mye fantastisk før det også, en av mine favoritter er Pan's Labyrinth. Skumle saker. Men han har tidlig i sin karriere faktisk touchet innom matematikk også. Geometria er en kortfilm fra 1987 fra samme regissør. På imdb leser vi at historien går ut på

A boy is tired of failing geometry, so he summons a demon.

Her snakker vi plot for en film! Filmen er rundt åtte minutter lang og et er kanskje ikke helt lov, men du finner den iallfall ganske lett på YouTube.

Blogger om matematikklæring

Her er noen av bloggene jeg leser. Alle har det felles at de omhandler matematikk eller læring av matematikk. Jeg kjenner ikke alle disse personlig, derfor kan jeg heller ikke alles fulle navn.) Legg gjerne inn tips til flere, for her har jeg glemt, oversett (og ikke hørt om) mange!

Matematikksenterets bloggarkiv:
http://www.matematikksenteret.no/bloggarkiv/

Bjørn Smestad:
http://larerutdanneren.blogspot.no/

Mike Naylor
http://mike-naylor.blogspot.no/

Simon Spurkland
http://mattelaereren.blogspot.no/

Tor Espen Kristiansen
http://torespensblogg.blogspot.no/

Elisabeth Engum
http://pgelisa.wordpress.com/

Karen Kristine
http://matematikklererensverden.blogspot.no/

Sean Martin
http://seanpkm.blogspot.no/

Andreas Holmstrøm
http://mattemonsteret.wordpress.com/

Og så noen utenlandske:

Kate Novak: A function of time
http://function-of-time.blogspot.no/ (US)

http://matteproblem.wordpress.com/ (Sverige)

Mathematics and multimedia
http://mathandmultimedia.com/ (US)

Math for love
http://mathforlove.com/ (US)

Math Munch
http://mathmunch.org/ (US)

Mathematics, learning and web2.0
http://colleenyoung.wordpress.com/

Research in practice
http://researchinpractice.wordpress.com/

PhotoMath. Eller Omkved. Eller: gammel diskusjon for n'te gang.

En ny applikasjon, PhotoMath (for iOS) får nå omtale i hytt og pine etter å ha lansert muligheten til å løse likninger ved å knipse et bilde med mobilkameraet. Du holder telefonen over likninga i ei eller annen bok, tar et bilde av likninga og vips så løses den. Du får til og med alle stegene underveis listet opp.

Utgivelsen har utløst et skred av omtaler (se her for adressa.no sitt første oppslag, eller Free Tech for Teachers eller Lifehacker.com eller Phandroid eller...ja, du skjønner tegninga) og viraken kan i det hele tatt minne om mediaomtalen Dragonbox fikk (og det tre ganger, siden firmaet så langt har gitt ut tre apper som alle ble en hit i media). Det vil si, først måtte vi gjennom en periode der mange uttalte seg (kanskje uten å ha prøvd appen - slik jeg skal gjøre nå) og så var det en periode der svært mange kastet seg på bølgen (og andre litt mer nyansert og kritisk) og så viste seg at det ikke var så effektivt å undervise med Dragonbox, da. Så kunne vi som ikke skal anvende appen direkte bare sitte i ro og mak og vente på at resultatene peker enten ene eller andre veien.
Lenkene i teksten over er bare et bittelite utplukk av oppslag om Dragonbox og det gjenstår å se om PhotoMath kommer til å få like mye oppmerksomhet.

Nå tenkte jeg å gjøre det enhver arrogant debattant ville ha gjort - og gjør - nemlig å rakke ned på PhotoMath uten å teste den selv. Så får jeg eventuelt laste den ned når den kommer i et skikkelig format (altså for Android-plattformen).

Men hvorfor så kritisk? Spesielt uten å ha prøvd den!?

Vel. Når de ikke lager Android-app kan de ha det så godt! Neida. Men NÅR Android-appen kommer skal jeg iallfall laste den ned og se om jeg kan bli positivt eller negativt overrasket ut fra fordommene som presenteres nedenfor.

Først det rent matematiske i appen. Et Googlesøk avslører ganske raskt feil som kanskje kan rettes opp i neste versjon, eller kanskje ikke. For eksempel har Dan Meyer skrevet et blogginnlegg der applikasjonen rett og slett roter til veldig enkle oppgaver. Der ser vi at det er fort gjort at appen surrer med variabelen x og gangetegnet x. Et av svarene som kommer som en konsekvens av det er ikke en gang logisk konsistent. Og det er tross alt en ganske viktig forskjell. Da er det nok bedre å bruke den norske standarden for gangetegn (en prikk).

Appen har fått mye negativ mottakelse denne gangen (altså stikk motsatt av Dragonbox), med begrunnelse i at dette kan brukes til å fuske på eksamen og prøver. Ja, hvis omstendighetene tillater at elever sitter og knipser bilder under en prøve... (får de virkelig lov til det?)... så er ikke det akkurat positivt. Men likevel synes jeg ikke dette i seg selv er så ille. Prøvesituasjoner må uansett tilpasses de hjelpemidlene som er tilgjengelige eller de som bør være tilgjengelige. Jeg kan nesten ikke skjønne dette argumentet med at PhotoMath automatisk er fusk. Det kommer jo helt an på! Alle mulige teknologier blir som regel slaktet på grunn av at de kan brukes til fusk, spesielt før man finner ut hvordan man skal håndtere de. Det må gå an å se litt forbi dette problemet, det kan ikke være så vanskelig å takle det at noen KAN fuske med denne appen.

Men sett at applikasjonen hadde virket da, og er feilfri. Ville den da vært brukandes? For tekniske vanskeligheter er jo noe som ofte kan utbedres. Altså, sett at applikasjonen _kan_ løse likninger? Hvilke likninger kan den løse? I The Big Bang Theory får vi høre om The Lenwoloppali Differential Equation Scanner,  det vil si en applikasjon som kan skanne en differensiallikning og løse den. Her er nok diff.likninger valgt litt for å være morsom på bekostning av Howard (som "bare" er ingeniør), siden han har mest med den typen likninger å gjøre, og at det også ganske ofte eksisterer metoder for å løse et stort antall av slike likninger. Det kan være ganske avanserte teknikker, riktignok. På dette nivået er selvsagt ikke PhotoMath. Riktignok har kalkulatorer kunne løse avanserte likninger symbolsk i lang tid, jeg husker selv at dette kunne gjøres på min første avanserte kalkulator, en HP48, som jeg kjøpte på tidlig nittitall. 

Bilde fra Wikipedia

Denne kalkulatoren brukte det som man kalte "Pretty Print", som gjorde at man kunne skrive inn likninger slik de stod i boka. Selv om kalkulatoren var basert på omvendt polsk notasjon kunne den altså andre triks også.

OK, en avansert kalkulator kunne løse vanskelige likninger, hva så? Jo, PhotoMath kan ikke akkurat løse verdensproblemer. Greit nok. Den kan ikke bevise Riemannhypotesen. Greit nok, det også. Og den kan for all del ikke løse diff.likninger som i Big Bang Theory. Det kan for øvrig websider som Wolfram Alpha, eller apper som GeoGebra og wxMaxima og... stort sett de fleste matematikkapper. PhotoMath kan egentlig ikke gjøre så mye annet enn å løse likninger som er skrevet i veldig pent trykk i niendeklassebøker (mer eller mindre), og det er kanskje ikke så nøye om det fins en app som, de gangene den virker, løser slike oppgaver. Jeg tror verken den revolusjonerer undervisning og læring, eller forårsaker spesielt vanskelige vurderingssituasjoner. Men det kan jo tenkes vi må tenke enda litt mer på hvordan man underviser og vurderer. Men det tåler vi vel?

Er du redd for fusk kan du vel bare gi håndskrevne oppgaver? Er du redd elever kan misbruke PhotoMath for å unngå å lære? Da kan du vel bare lage oppgavene slik at applikasjonen ikke er anvendelig da. Hvor ofte i livet kommer du ut for å måtte løse likninger som er sirlig oppstilt og trykket på papir? Hint: aldri. Under læring av likninger er det sjelden standard algoritmer og svar er viktigst. Algoritmene gir deg kokebokoppskrifter som kan følges enten du forstår det eller ei, og da er det mye bedre at elevene får (hjelp til å) utvikle tenkning som gjør at slike problemer gir mening. Og hvis svarene er viktigst? Vel, de står som regel bakerst i boka også... Hvis likningsopplæringen består av å lære algoritmer er det kanskje ikke så stor forskjell hvis man delegerer det til en app å vise hvordan det skal gjøres.

Etter alt det vi vet om det å lære matematikk fra de siste hundre (?) år med forskning så er vel noe de fleste enes om at man trenger å forstå matematikken for å kunne anvende den i ukjente situasjoner og man trenger også å beherske mange ferdigheter (fortrinnsvis for å anvende i kjente situasjoner). Tenk på det slik: Elevene må få trening i å håndtere problemer der det ikke eksisterer noen kjent framgangsmåte, og de må få trening i å etablere en del standard ferdigheter som f.eks. å kunne gjengi resultater i gangetabellen relativt raskt. Jeg ser ikke at PhotoMath kan hjelpe til med noen av delene.

Så gjenstår det bare å teste appen, når den kommer (og jeg forventer at flere av påstandene over blir motbevist! :-) ). Om jeg skal trekke noe positivt ut av at slike applikasjoner kommer så må det være at tilgjengeligheten nå er så bra (eller dårlig, om man ser slik på det) at hvem som helst kan ha slike muligheter for hånden. Ikke alle hadde en HP48 på nittitallet. Tror ikke engang alle lærerne på den tida hadde hørt om den. At hvem som helst nå har en likningsløser lett (og poenget her er LETT) tilgjengelig fører til at lærere og lærende må ta stilling til teknologien og ikke late som om den ikke eksisterer eller prøve å holde den skjult for andre.

Søndagsblogging: Fra siste ukes sløsing av tid på Internett...

Her er det jeg fant på nettet i uka som gikk!
(Ikke alt, da...)

Slik tegner du perfekte sirkler:
http://www.sciencedump.com/content/how-draw-perfect-circle-freehand. Når du har perfeksjonert teknikken kan du se om du kan utfordre mesteren: https://www.youtube.com/watch?v=eAhfZUZiwSE.

Knoema World Atlas, visualiseringer om diverse datamateriale fra verdens land
http://www.freetech4teachers.com/2014/10/knoema-world-data-atlas-reference-data.html#.VE0rWfmG-Sp

Språkpirk, en blogg om språkets finurligheter, fra Stian på HiST!
http://mattegreier.blogspot.no/2014/10/sprakpirk.html

Også deltok jeg på MatRIC sin workshop om å lage video i matematikkfaget, i Bergen:
http://www.uia.no/senter-og-nettverk/matric/activities/mathematics-video-tutorial-workshop

Marit Larsen spurte "Can you calculate in space and time?"
https://play.spotify.com/track/43gYflbNTKCeJhqgmt17Br?play=true&utm_source=open.spotify.com&utm_medium=open

Wordle

Dette er kanskje ikke all verdens nyttig, men slike ordskyer som man kan lage på Wordle er ganske morsomme! For eksempel kan du kopiere hele teksten fra oppsummeringen av den amerikanske læreplanen ("Standards") og lime den inn i Wordle for å få denne ordskyen. Hva ser ut til å være de viktigste tingene i læreplanen?
Hva med den norske? Her er læreplanen i matematikk, altså Kunnskapsløftet. Hva legger vi vekt på her til lands?

Lag dine egne ordskyer av en hvilken som helst dunge av tekst - hva forteller ordskyen?

Matematikkvitter

På trøndersk prøver jeg å få innført betegnelsen "tvittjer", men det går litt sakte... Uansett - her er noen av twitterfavorittene relatert til

matematikkverdenen! Kommer til å oppdatere denne etter hvert om hukommelsen strekker til!

På norsk:
Matematikkfakta
NDLA Matematikk
NooA Matematikk
Jo Røislien
Matematisk institutt, UiB

Kanskje litt mer naturfagrelatert:
Selda Ekiz
Kunnskapsløypa

På engelsk:
MyMathCloud
Plusmath
Republic of math
Museum of math
Math 4 everybody

Lærere i matematikk:
Simen Spurkland
Elisabeth Engum
Sigbjørn Hals
Tor Espen Kristiansen
Ida Vetleseter Bøe
Helle Lund Olsen
Christian Johansen
Anders Fossen Trøan

Lærerutdannere i matematikk:
Line Rønning Føsker

Bjørn Smestad

Reidar Mosvold
Svein Arne Sikko
Torkel Haugan Hansen
Siri-Malén Høynes
Elise Klavenes
Tore Forbregd

Litt generelt for lærere:
Lærerråd

Det fins også lister man kan følge, der mange brukere er "tvangsinnlagt" som lærere, forskere, matematikere... osv:

Spill: CrossMe

EDIT: Dette spillet kostet visst noen kroner likevel, for en gratis versjon kan du se nederst i posten.

Cross Me er nok en type puslerier som er som skreddersydd for nettbrett. Ja, for det er faktisk litt knotete på en liten telefonskjerm, der man må zoome litt her og der for å få til å trykke på rett sted.
Dette spillet har helt sikkert sin analoge opprinnelse, men jeg klarer ikke å finne ut hva det heter. Jeg synes å minnes at det er kinesisk eller japansk, men er usikker. I følge http://en.wikipedia.org/wiki/Nonogram er Hanjie eller Griddlers navn på papirutgaven, men jeg klarer ikke huske at det var slik...
Når du starter spillet presenteres du for et rutenett som du skal fylle inn. Tallene på siden angir hvor store rekker som skal fylles inn. På bildet under er det for eksempel slik at det i øverste rekke skal fylles ut fem ruter, det vil si alle. Et lurt sted å begynne. Tredje og femte rekke er også innlysende, samt første kolonne. Så da er man godt i gang!

Spillene blir litt mer omstendelige etter hvert som både størrelsen på rutenettet økes, og man også må fylle ut flere serier i samme rekke eller kolonne. Her ser du at det i øverste rekke skal fylles ut to ruter, men de skal ikke henge sammen - og må altså stå som to separerte ruter.

Etter hvert begynner mønsteret å ta form, her er et delvis løse puslespill på tjue ganger tjue ruter. Taktikkene kan likne litt på sudoku, for man er ofte like opptatt av å fylle inn hvor det IKKE må fylles ruter. På samme måte som man i sudoku gjerne noterer seg hvilke tall som ikke kan stå i ei bestemt rute.

Litt mer utfylling og løsningen er klar!

Du finner spillet på Google Play her: https://play.google.com/store/apps/details?id=com.mobiledynamix.crossme&hl=no

EDIT: Etter å ha kikket rundt på Google Play endte jeg opp med følgende variant, som fungerer kjempebra - Griddlers Plus. Det fungerer omtrent som spillet nevnt over, du blir presentert med en grid som denne:

Også her gjelder det å fylle inn rutene gitt ved tallene på sidene. Skipet over ser slik når alle rutene er riktig utfylt:

 Det er massevis av bilder å løse her, men et lite drawback er at de avanserte spillene er ganske vanskelig å få gjort på en mobiltelefon så det er definitivt en fordel med nettbrett og kanskje stylus.

Se om dette kan være noe for deg på https://play.google.com/store/apps/details?id=com.ally.griddlersplus !

Språkpirk

Ikke så mange kolleger på lærerutdanningen blogger, så vidt jeg vet (prove me wrong!), men de få som er må vi bære fram på gullstol! Stian på norskseksjonen har en blogg som jeg antar er hans yndlingsprosjekt! Den heter språkpirk og her _kunne_ man jo tenke seg at det skulle bli delt ut verbal dæng til de som ikke følger gitte normer og regler... Det viser seg heldigvis at bloggen har et selvpålagt mandat mer i folkeopplysningens ånd, nærmere bestemt å sette fingeren på små finurligheter i språket vårt. Du vet, slike ting vi ofte plages litt med når vi skal skrive korrekt. Hva er flertall av dinosaurus? Heter det klokketro eller klokkertro? 

Sjekk Språkpirk på http://sprakpirk.info/

Får du ikke nok språkpirk fins det mye å ta av!

Proofs without word - redux

En gang hadde jeg et innlegg på Novemberkonferansen der jeg nevnte sjangeren "Proofs without words", eller "bevis uten ord". Dette er en spesiell måte å bevise ting på i matematikk, der man lar en figur tale for seg. Har også laget noen slike ordløse bevis i GeoGebra og PowerPoint. Poenget er likevel at man er nødt til å tenke ganske grundig gjennom disse påstandene for å forstå de. En fin måte å jobbe med det er å la elever eller studenter to og to (neppe fler) snakke om det som skjer på bildene eller GGB/PPT-filene.

Det fins  flere bøker om slike ordløse bevis, og to av dem er skrevet av Roger B. Nelsen og kan kjøpes for en rimelig penge på f.eks. Amazon.com.

Dette beviset er hentet fra en samling jeg oppdaget på Mathoverflow.net. Her skal man vise at

\( 1+2+3+ \dots +(n-1)=\binom{n} {2} \)

Symbolet \( \binom{n} {2} \) betyr "antall måter vi kan velge ut 2 av en mengde med n objekter på" (Uten å legge tilbake de vi velger, og uten å bry oss om at det er viktig hva som blir trukket først og sist). 

Hvordan kan vi bruke animasjonen over til å se at påstanden er riktig?

Her er enda flere animasjonsforklaringer:
21 GIF-animasjoner som forklarer matematiske sammenhenger.

En bråte animasjoner fra Wikipedia

Visually stunning math concepts which are easy to explain

En glipp

I dag må jeg innrømme litt dårlig samvittighet. En gjennomgang av lokale saker i avisa i morges fikk meg til å knise litt, da det viste seg at på min datters skole hadde lærerne sendt med elevene lekse om å finne ord på E på et bilde av en elefant m.m.

Problemet var bare at "m.m." i dette tilfellet betydde blant annet "ereksjon" og "ejakulasjon" og kanskje enda mer oppfinnsomme ord på E dersom man leter litt. Jeg syntes dette var ganske morsomt og delte saken på Facebook. Vi spøkte litt om dette, elefantens mangel på støttenner ble f.eks. nevnt (lærer ikke lærere om støttennende stillas lenger? Tji-hi), men altså, i det store og hele var det jo mest morsomt. Vi spekulerte også litt på hvordan lærere kunne være så sløve at de ikke oppdaget dette da de laget leksa.

Men så kom den ene nettavisen etter den andre og skrev om denne etter hvert berømte leksa. Facebooksida "Idebank for småbarnsforeldre" kom også raskt på banen, og flere steder finner vi også det alltid raskt tilkommende kommentarfeltet (også kalt "kloakken") der de fleste så ut til å vite godt hva som feilet dagens skole, hvor store idioter lærerne var og hvor forferdelig det var at slikt kunne skje. Adressa måtte få tak i en sexolog til å si hvor ille dette var og de sporet opp kunstneren som tegnet tegningen for ti år siden. Kunstneren selv sier at dette er for voksne, og selvsagt ikke var et bilde som var ment for barn i det hele tatt (jeg har prøvd å tolke dette bildet som voksen, uten helt å skjønne hva kunstprosjektet innebar, men det for nå så være - det er en grunn til at jeg bare er lærer i matematikk...).

En stemme kommenterte på innlegget jeg delte noe sånn som at "så flott, nå kan lærerne bli enda mer hengt ut", og jeg slettet straks min deling av saken, med en flau smak i munnen. Så enkelt kan det sies.

På skolen hører ungene våre om at informasjon kanskje ikke trenger å sendes videre i alle sammenhenger, og det må iallfall være både sant, godt og nødvendig (Les legenden om Sokrates her). Her er det iallfall hverken godt eller nødvendig å henge ut disse lærerne som begikk en slik glipp. Og selv om det er sant at dette skjedde er det nok ikke noe NOEN har nytte av å vite utenfor kretsen av de som har med denne skolen å gjøre. Det er helt greit at foreldrene sier fra _til lærerne_ (det skulle bare mangle), og lærerne er lei seg og skjønner dette ikke skulle ha skjedd. Så er saken ute av verden.

Det slår meg hvor vanvittig lett det er å begå en glipp som andre kan sikle om kapp over. Og hvor lett - kjempelett! - det er å dele en slik glipp videre. På vår institusjon, en lærerutdanningsinstitusjon må vite, var det en lærer som kom i skade for å dele et ord feil på en kjapp melding som ble lagt ut på it's learning. Knappest verdens undergang, men en student fant det likevel på sin plass å ta bilde av hendelsen og rapportere det til Facebook-gruppa "Astronomer mot orddeling" (Gjenta sutringen omkring kommentarfelt, skrevet et par avsnitt lenger oppe). "Slikt kan ikke skje på en lærerutdanningsinstitusjon" osv.

Altså. Uansett hva journalister måtte mene, elevene fikk ikke sex-lekse. De fikk en glipp. En morsom liten glipp, men fnis ferdig og move on. Det skal jeg gjøre. Å dele dette på facebook er isolert sett ikke noe som man skulle tro spiller så stor rolle (For det er jo bare mine venner som ser det. Og deres venner. Og deres og... ups).

Lærere og norsk skole er ikke tjent med, og fortjener ikke at en humoristisk Google-glipp skal gi foreldre og medier en ny mulighet til å svartmale lærerprofesjonen, lærere og skoleverket. Tror ikke noen synes dette er morsomt hvis involverte lærere skulle bli sykmeldt og deprimert av all omtalen.

Egentlig fikk kunstneren bak bildet sagt det ganske greit:

- Bildene er ment for voksne, og ikke for barn. Jeg synes litt synd på læreren som har googlet seg fram til dette bildet uten å se så mye på det, sier Henriflette.

Nytt på nytt, hold dere unna. En dags oppmerksomhet får holde, og jeg føler meg _rimelig_ sikker på at dette ikke skjer igjen, for å si det sånn.

(Et lite forbehold: Skulle det være slik at det var en fjøsnisse av en lærer som tenkte at dette bildet var morsomt å sende med ungene for å skape litt flau stemning hjemme... så still deg i skammekroken og står der til Paradise Hotel er ferdig.)

Spill: Wuzzit Trouble!

The Wuzzits need you! Det fins en bråte apper for å jobbe med matematikk og for å lære matematikk. Det kanskje best kjente eksemplet nå for tiden er nok Dragonbox (De siste ukene har det nok riktignok handlet mest om at elever _ikke_ ble bedre i algebra av Dragonbox. Her trengs det riktignok en del flere studier, men artikkelen fra tangenten var iallfall ikke videre positiv. Her er rapporten den bygger på). 

Keith Devlin er en anerkjent fagdidaktiker i matematikk. Han har skrevet en hærskare av bøker, både innenfor vitenskapsfaget matematikk, fagdidaktikk og rent populærvitenskaplig. (Min favoritt er nok  the language of mathematics). Spennende er det da at han har stått bak utviklingen av spillet Wuzzit Trouble, som du finner både til Android og iOS-enheter. 

Spillet følger de vanlige skjemaene med at man får en til tre stjerner for hvert gjennomført brett, og må låse de opp etter hvert som man turer fram. Akkurat som Angry Birds og alle de der. 

I dette spillet er oppgaven din å trekke opp et hjul med et bestemt antall omdreininger. Når du slipper snurrer hjulet rundt og får et større hjul til  bevege seg i motsatt retning.

Hensikten er å få snurret det store hjulet slik at nøklene i tur og orden havner øverst der den grønne trekanten er. På bildet over ser du tallet fem på det lille hjulet. Det vil si at hver omdreining du trekker det opp med får det store til å flytte seg fem hakk i motsatt retning. Vi ønsker at det store hjulet skal flytte seg først 5, så 5 til, så 5 til og så 5 til. Da har det store hjulet stoppet opp på både 5, 10, 15 og 20 og alle nøklene blir låst opp. Vi kan altså løse oppgaven ved å trekke det minste hjulet rundt fire ganger. 

På bildet over har vi snurret det minste hjulet rundt en gang i negativ retning. Når vi slipper spinner det i den oransje pilens retning og får det store hjulet til å snurre slik at det står 55 øverst og nøkkelen er fri.

Det deles ut stjerner og det er om å gjøre å bruke minst mulig trekk for å låse opp alle nøklene.

På bildet over ser vi at vi må snurre først den ene veien og så den andre. Eller klarer vi å komme helt rundt ved å snurre en og samme vei? Vi kan maks trekke opp det lille hjulet med fem omdreininger...

Dette spillet virker passe meningsløst til å begynne med, men etter hvert ser man at man virkelig må tenke logisk før man trekker opp det lille hjulet med riktig antall snurr i riktig retning. Det er litt vanskelig å forklare, her er det bare å prøve selv!

Last ned til Android eller iOS!

Hjelp Simon!

Simon har en blogg med omtrent samme tittel som min, så da er det bare rett og rimelig at jeg hjelper til litt med å finne informanter! Se her: http://mattelaereren.blogspot.no/2014/06/trenger-informanter-til-masteroppgave.html

HiST-Kolleger som blogger

Jeg tenkte å samle sammen det jeg fant av kolleger som blogger. Jeg vet at det f.eks. på AiTEL er kultur for blogging på f.eks. ITfag, mens vi på lærerutdanningen så langt ser ut til å være mer individualister...

Harald Morten Iversen:
Harald Morten er på norskseksjonen på HiST. Jeg aner ikke hvilken språksjanger han vil definere bloggen sin som, tør jeg gjette Lingvistikk? Og grammatikk? Og dialekter? Og litt skryt om hvor flink han er til å jogge.
http://my.opera.com/Haraldmi/blog/

Per Bjørn Foros:
Per Bjørn blogget vel egentlig ikke HELT selv, siden jeg satte sammen noen av tekstene han sendte over til en blogg. Men de er god lesning uansett. Per Bjørn driftet i mange år Rørosseminaret og på et tidspunkt kom også behovet for et nettsted tilknyttet seminaret. Jeg foreslo å bruke Google Sites for å lage det selv og han ble etter hvert så durkdreven i gamet at han liksågodt tok over hele webmasterjobben (han foretrekker tittelen webherre) for Rørosseminaret og driftet dette knirkefritt, med påmelding, hotellbestillinger og det hele.
Rørosseminaret: http://www.rorosseminaret.no
Friherren: http://perbjorn.wordpress.com/

Michael Naylor:
Jeg jobbet sammen med Mike i et år på HiST da han hjalp oss med et matematikkurs. Han er til daglig ansatt på Matematikksenteret, men har ekstremt mange baller i luften samtidig (han er forsåvidt også jonglør...). På bloggen kan du lese om både faglige og private opplevelser fra livet i Norge (Mike er amerikaner. Eller er han norsk nå? :) ). Mike har verdensrekord for verdens lengste publiserte ord og advarer alle sterkt mot å kjøpe boka si, Abacabadabacaba. Av andre prosjekter kan jeg også nevne http://www.shapeways.com/designer/MikeNaylor, virksom type, dette!
Naylors in Norway: http://naylors-in-norway.blogspot.com/
Mike har også en matematikkblogg. Denne finner du på http://mike-naylor.blogspot.no/

Ola Erik Domaas:
Ola Erik jobber på RLE-seksjonen og blogger mest om akkurat det, nemlig religion, livssyn og etikk. Som ateist er det godt å ha kolleger som kan skrive åpent og inkluderende om disse temaene, til tross for våre divergerende livssyn!
Olas observasjoner: http://oladomaas.blogspot.com

Jan Frode Haugseth:
Jan Frode leder i skrivende stund et IKT-prosjekt for HiST og er ansatt på Pedagogikkseksjonen. Han blogger på http://jafro.org/

Stian Hårstad:
Fra norskseksjonen kommer også en språkpirk-blogg! Er det noe du irriterer deg over at folk skriver feil vil det nok dukke opp i Stians blogg!
http://sprakpirk.info/

Håper jeg kan føye flere kolleger til listen etter hvert! (Send meg gjerne tips, HiST-ALT'ere!)

Spill: 2048

Da var påska ødelagt. Egentlig - sånn EGENTLIG - er jeg ingen spiller, til tross for at noen poster kanskje skulle tilsi noe annet. Jeg har tidligere skrevet om en og annen app og noen spill med matematikkrelatert innhold. I litt vid forstand. Her er et nytt.
Spill som har høy avhengighetsfaktor trenger som regel ikke å promoteres noe særlig, de bare tar av og lar Internettet gjøre jobben. Det tror jeg skjer her. Jeg hadde ikke hørt om spillet før jeg så en tilfeldig tweet om det. Lastet det ned og fikk så en fornemmelse av at ALLE hadde spilt det eller spiller det. Vel, slik er det kanskje med mange ting. Du har kanskje vært utenlands på et nytt sted, og når du kommer tilbake virker det som om du kan lese om dette stedet overalt. Jeg tror dette er et ganske finurlig læringsprinsipp, selv om det kanskje ikke står så mye om det i pedagogikkbøkene! I bunn og grunn tror jeg ikke at vi som lærere kan legge noe som helst av kunnskap inn i hodet på andre, MEN jobben vår er å legge til rette for at kunnskap kan utvikles, OG - og dette er det viktigste - vi må lede elevenes oppmerksomhet mot det som skal læres. Slik kan vi etterpå si at eleven har lært hvis han/hun nå raskere retter oppmerksomheten sin mot tilsvarende fenomen.

Ok, et lite sidespor det der.

Dette spillet er enkelt. Du spiller på 4 x 4 ruter og starter med to to-tall.

Her skal du så sveipe/swype brettet i en av de fire himmelretningene slik at like tall kræsjer sammen. Når du sveiper flyttes alle brikkene i retningen du sveiper, helt til de stoppes av veggen eller andre brikker. På bildet under har to toere kræsjet sammen til å bli en firer. I tillegg har de dukket opp en toer to ganger til, og nå kan jeg sveipe oppover for å få disse to til å suse sammen.

Og slik fortsetter det. For hvert sveip dukker det opp et nytt to-tall et sted. Her er jeg godt i gang og har fått en 512'er!

Klarer du å holde det gående helt til du får en 2048'er har du vunnet. Her er brettet fullt, og det er ingen like tall ved siden av hverandre. Da er nok spillet tapt, gitt. 

Spillet er gratis og finnes i mange omtrent like versjoner. Jeg lastet ned den på https://play.google.com/store/apps/details?id=com.estoty.game2048. Men du kan også prøve f.eks. https://play.google.com/store/apps/details?id=com.digiplex.game. For iOS finner du det på https://itunes.apple.com/us/app/2048/id840919914?mt=8 

Så hvordan kan dette relateres til mine ramblings om læring og oppmerksomhet? Vel, spillet leder definitivt oppmerksomheten mot dobling, selv om det i dette tilfellet ikke er dobling som skal læres. Dobling er en kraftig strategi når elevene senere skal utvikle egne måter å finne svar på regnestykker på. Slik kan vi godt kaste bort noen minutter med dette spillet, men likevel håpe vi kan sitte igjen med en endret oppmerksomhet mot dobling etterpå!

God påske!

EDIT: Klarte det endelig! (Jada, jeg er litt treig...)

Brannfakler og Dragonbox

Dragonbox (http://www.dragonboxapp.com/) er muligens det digitale spillet som har blitt mest hauset opp for bruk i matematikkundervisningen. Det har blitt markedsført ganske tungt, fått massiv oppmerksomhet i inn- og utland, og vært i utallige aviser og reportasjer.

Selve spillets gang er ikke noe nytt. Man får en situasjon, skal gjøre det samme på begge sider og finne ut hva som skjuler seg i en beholder man ikke får se inni. I Algebra för alla (Bergsten et.al, 1997) har vi en snart tjue år gammel behandling av en konkret versjon av likningsspillet. Boka er middels vanskelig å få tak i, så du kan også se litt i denne artikkelen fra NCM (tilsvarer omtrent Nasjonalt senter for matematikk i opplæringen i Sverige):
http://ncm.gu.se/pdf/namnaren/0710_08_4.pdf. Det er fortsatt populært å bruke fysiske, konkrete versjoner av dette spillet uten at vi trenger digitale verktøy til dette. Og for all del, selv om jeg i farten ikke vet hvor likningsspillet kommer fra, er det nok kjent fra lenge før 1997!

Nå har Dragonbox gått sin seiersgang over verden, møtt stor begeistring og beskjeden kritikk, etter hva jeg kan se. Selv har jeg plassert meg litt sånn på ignoramus-linja, skeptisk inntil jeg ser noen grunn til at det skal funke, men også åpen for tanken om at det kan være artig å bruke det, og forhåpentligvis nyttig. Jeg har kjøpt spillet og spilt gjennom det, og også latt husets femåring frese gjennom. Hun er muligens en av unntakene, som ble lei etter de første femten brettene, men jeg ser det er eksempler i hopetall på barn som har pløyd gjennom hele spillet på kort tid og som har vært motiverte for det.

Jeg skal ikke analysere spillet, men kjapt oppsummert, du får oppgaver som i starten er simple og tilsynelatende langt unna matematikklandskapet. Sakte, men sikkert nærmer du deg matematikken ved at kompleksiteten og representasjonene endres. Av det jeg likte var at det fokuserte veldig på at det hele tiden må gjøres likt på begge sider, en fundamental tanke i likningsløsningen, selv om det også fins steder der man roter seg bort i denne tankegangen. Det jeg ikke liker så godt er prinsippet om at symboler og algoritmer som er fremmede for eleven, slik som likningsalgoritmen og algebrasymbolene i matematikken er, nå blir byttet ut med et nytt, forholdsvis meningsløst representasjonssystem og regelverk. Man kan ikke gjøre nøyaktig det samme med likninger som med Dragonbox og jeg tror mye av hypen ligger i at media har omtalt det som en erstatning av likningsundervisningen, mens det sannsynligvis ikke var ment slik.

På hjemmesidene til appen reklameres det at man kan lære Algebra Basics på få timer. Jeg kan ikke fatte og begripe at det skal gå an, og jeg må bare tenke at da har man nok en annen definisjon på læring enn det jeg tenker bør være rådende i skolen.

7.7 millioner likninger løst på kort tid. Noe av det jeg husker med gru fra barndommen er denne konkurransen der det er om å gjøre å bli først ferdig. Kappregning, som det omtales som i Geir Bottens bok Meningsfyllt matematikk

Nå har det vært en undersøkelse i Dagens Næringsliv, der læringsutbytte av Dragonbox sammenliknes med tradisjonell undervisning (http://www.dn.no/meninger/debatt/2014/04/23/Skole/dataspill-og-lringsutbytte). Det er i det hele tatt livsfarlig å skulle foreta forskning som dette, man kommer gjerne til konklusjoner det er vanskelig å backe opp. Kompleksiteten i klasseromsituasjoner gjør at sammenliknende forskning ofte er bortimot en umulighet og ofte ikke engang er ønskelig.

Ønsker du å se hvor "tråkig" man KAN lage en likningsapp, kan du kanskje heller se på denne: http://www.skolresurs.fi/matteva/algebra/ekvationsShooter.html :)


Litt.

Bergsten, C., Häggström, J., & Lindberg, L. (1997). Algebra för alla. Göteborg: Nämnaren NCM Göteborgs universitet.

Botten, G. (2003). Meningsfylt matematikk: nærhet og engasjement i læringen. Bergen: Caspar forlag.

Boktips: Tall forteller

Tall forteller er skrevet Jo Røislien og med Kathrine Frey Frøslie som medforfatter. Begge er statistikere. Jo Røislien er kanskje mest kjent for folk flest fra TV-serien (og boka) Siffer, som gikk på NRK. (Du kan se serien på nett-TV her: http://www.nrk.no/skole/programdetalj?topic=nrk:program/siffer .)

I Tall forteller går forfatterne gjennom de mange ulike måter man kan foreta undersøkelser på, som f.eks. spørreundersøkelser eller andre empiriske datainnsamlinger. De forskjellige typer undersøkelser blir kategorisert og sortert og vi kan lese om hva som kjennetegner disse. Her finner vi faguttrykk som deskriptiv statistikk med en variabel, kontinuerlige variable osv.

Boka er lagt opp nesten uten matematikk, og det kan kanskje virke rart for noen. Ikke en gang hvordan man regner ut gjennomsnitt blir vist fram for leseren, men det legges vekt på å tolke resultatene og å tolke beliggenhetsmål som gjennomsnittsmål og median og spredningsmål som bredde og varians.

Som sagt, det kan virke rart å snakke om alle disse begrepene - som egentlig har ganske lange matematiske utregninger hengende ved seg - uten å ta de med. Men det som gjør denne boka ganske original er at det hører med en app som gjør akkurat dette. Denne kan du laste ned gratis på https://play.google.com/store/apps/details?id=no.tallforteller.app. Her kan du sette opp dine egne spørreundersøkelser og få ut dataanalysene veldig lett. Boka gir eksempler på hver eneste type undersøkelse og viser hvordan du bruker appen for å samle og analysere data. Tøft.

Jeg vet ikke helt hvem denne appen egentlig passer best for. For den som skal gjøre seriøse undersøkelser blir det nok litt for light. For elever blir den kanskje utilgjengelig, dersom disse ikke har tilgang til telefoner eller nettbrett. Det er mulig P-kursene i videregående skole er midt i smørøyet her, selv om det i VGP selvsagt også hører med en del regning når man jobber med dette stoffet.

Selv om jeg kjenner til de undersøkelsestypene som gås gjennom er det fint å få veldig enkle eksempler på hver type, samt å se eksempler som sannsynligvis vil være av interesse for unger og ungdommer. Blant eksemplene kan vi finne en undersøkelse som illustrerer Bivariat analyse: to grupper med kategoriske binære data. Det høres jo ut som en munnfull, men undersøkelsen tar for seg hvordan man kan bruke appen og statistikken til å undersøke om det er VG eller Dagbladet som er den mest tabloide avisen. Selve undersøkelsen går ut på å telle over tjue forsider og notere i appen hvor mange av forsidene som inneholder ordene "du", "deg" eller "din".
Etter undersøkelsene nevnes det hvilke andre typer spørsmål du kan få svar på med samme teknikk, og i dette tilfelle kan vi bruke framgangsmåten om vi ønsker å finne ut om foreldrenes musikkinteresse påvirker om barn spiller i skolekorpset eller om speiding er like vanlig blant gutter og jenter.

Coggle

Å organisere tankene sine er ikke lett. Jeg har prøvd flere metoder for å organisere tenkningen min, og her skal jeg vise en av de jeg liker best for tida.
Jeg har ofte brukt tankekart for min egen del, og de siste årene har jeg på slutten av hvert semester gått gjennom semesterets pensum sammen med studentene og laget et tankekart sammen med dem. Det er vanskelig for meg å si hvor nyttig det er, men jeg ser at mange tar med seg teknikken videre, etterlyser en oppsummering av denne typen året etter - og sier generelt at de synes det er nyttig. Noen får også inspirasjon til å bruke det med elevene sine i praksisperiodene. Det enkleste har riktignok vært å dele ut A3-ark til studentene så de kan gå amok av kreativitet med tusjer, mens jeg selv tegner på datamaskin. Slik kan jeg lett dele med de som ikke var der, og også endre i etterkant. Og arkivere til senere år. Noen av studentene har også valgt å bruke digitale tankekart.
Jeg har prøvd programmer som MindMeister, Mind42, Xmind og Freemind. Ved HiST har vi i tillegg lisens på MindManager. Det fins også varianter for nettbrett, til og med for telefon, men jeg har ikke fått prøvd disse. Jeg ble imidlertid ganske overrasket over appellen til Coggle (coggle.it) da jeg prøvde det første gangen. Dette tankekart-programmet kjøres i nettleseren din (slik som de fleste andre nevnt over), men ser likevel litt annerledes ut.

Du har større frihet til å trekke greinene rundtomkring for å lage den layouten du selv vil. Og det er lett å fargelegge grener i de fargene du vil ha.

Klikk på ei grein og kontekstmenyen for fargevalg kommer opp. I tillegg til det layoutmessige er det et par egenskaper jeg har begynt å like spesielt godt i Coggle. For det første kan du legge in LaTeX-koder i tankekartet. Det betyr at YES! Vi kan putte inn matematikk i et tankekart!

Koden som skal settes inn er stort sett vanlig LaTeX-koder som de fleste som jobber innenfor realfagene kan være mer eller mindre kjent med. Forskjellen er at man må starte uttrykket med \\( og avslutte det med \\). Mellom der kan man skrive vanlig LaTeX. For å skrive gunstige delt på mulige, som på bildet over, skriver man \\( \frac{gunstige}{mulige} \\).

Man kan også sette inn bilder og lenker til nettsteder i tankekartet sitt. Noen ganger lenker jeg opp til artiklene fra it's learning, slik at studentene kan være pålogget der og havne direkte på de relaterte artiklene eller aktivitetene.
En annen stilig mulighet er at man kan lenke tankekart sammen. Slik kan man lage flere nivåer av tanker.

Her har jeg klikket på en grein, "emne", og fått menyen som plassert på sirkelen over. Øverst har vi et snodig tegn som sier "move branch to Coggle". Trykker vi på den så kappes hele denne greinen av og lagres som et helt nytt tankekart. Det vil da fungere slik at når du seinere trykker på greina "Emne" så lastes det nye tankekartet inn. Slik kan vi unngå at det blir altfor mye informasjon på ei side. 

Coggle kan kobles automatisk til Google Disk, slik at det er lett å dele tankekartene dine med andre, lett å ha de tilgjengelig sammen med de andre Google-greiene dine og greit å finne de igjen. 

Anbefaler deg å teste ut coggle.it 

Orden! Orden, sa jeg!

Her er ei webside med bilder fra ei bok som ser rimelig artig ut! En skal være forsiktig med å reklamere for bøker en ikke har lest, men dette så litt for attraktivt ut til å la passere.

Alle vet vi at livet bare er kaos, så her har vi en fotoartist som har sett det som sin oppgave å lage orden i kaoset. Alt fra sandkasser til grantre-greiner skal dissekeres og ordnes. Fascinerende.

Se utdrag fra boka på http://www.brainpickings.org/index.php/2013/03/28/the-art-of-cleanup-ursus-wehrli/

Bilde fra amazon.com

Kan bestilles på http://www.amazon.com/The-Art-Clean-Up-Life/dp/1452114161/?tag=braipick-20 , ser det ut til. Der finner du også hans (jeg tror det er et guttenavn!) andre oppryddingsprosjekter.