Nettfunn sist uke

Vanskelig å sammenlikne undervisningsresultater forskningsmessig
http://www.vg.no/forbruker/teknologi/skole-og-utdanning/lite-forskning-paa-laeringsutbyttet/a/23332904/

MOOCs fra store universiteter:
http://www.openculture.com/free_certificate_courses

Matematikksenterets blogg om Hunger Games
http://matematikksenteret.no/content/4639/The-Hunger-Games:-Mockingjay-Changes

Nettfunn sist uke

To sider av USAs utdanningsreform:
http://www.salon.com/2014/08/09/secrets_of_amazing_teachers_what_both_sides_of_the_education_reform_debate_get_wrong_about_autonomy_and_accountability/

Sorteringsalgoritme. Ganske stilig å se på.
http://9gag.com/gag/aPyoG4P

Neida, vi har ikke glemt at det er artig med papirfly!
http://www.sciencedump.com/content/tutorial-paper-airplane-actually-flies

Fibonacci
http://www.sciencedump.com/content/magic-fibonacci-numbers

Ikke kast TI-83'n - den kan spille spill!
http://nerdapproved.com/gaming/you-can-play-super-smash-bros-on-a-ti-83-or-ti-84-calculator/

Nettfunn sist uke

En flott tegneserie, "They used science". Sjekk også ut annet fra http://zenpencils.com/!
http://www.sciencedump.com/content/they-used-science-comic

Arne Kåre Topphol er førsteamanuensis ved Høgskulen i Volda (og ikke Volga, som det står i artikkelen), men han har lansert kritikk mot Überpedagog Hatties bruk av statistikk. Hattie på sin side svarer at han er klar over at halvparten av statistikken hans ikke holder. Underlig å fortsatt høste fruktene av slik massiv oppstandelse som han har forårsaket, uten å kommentere dette, er det ikke? Det gjør det iallfall ikke enklere å ta resultatene hans for god fisk.
http://ollieorange2.wordpress.com/2014/08/25/people-who-think-probabilities-can-be-negative-shouldnt-write-books-on-statistics/

En app som ser veldig handy ut! Ta bilde av ei eller flere sider fra ei bok og få resultatet lagt i dropboxen din som pdf.
http://mathandmultimedia.com/2014/11/08/genius-scan/
Android app her: https://play.google.com/store/apps/details?id=com.thegrizzlylabs.geniusscan.free&hl=en

Forklaringen på matematikkvitser...
http://www.sciencedump.com/content/math-jokes-explained

Derfor bruker vi X
http://www.gizmodo.com.au/2014/11/why-we-use-x-as-the-unknown-in-math/




Why is Math Different Now from raj shah on Vimeo.

Link til side i pdf

Relativt stor oppdagelse for meg, og noe som sikkert folk flest har visst i tiår. Er inne i en prosess med å samle sammen artikler og ting man har skrevet for å en dag kunne søke om opprykk. Da er det behov for å lenke til skribleriene sine. Problemet er når disse står langt bak i et svææært pdf-dokument. Så litt ut av det blå dukket løsningen opp.
Legg til en #page=69 (eller et annet sidetall) og leseren fraktes direkte til angitt side når man trykker på lenka! Smart :)
http://www.caspar.no/tangenten/2005/t2005-3.pdf#page=69 

Kolleger på twitter

Lærerutdanningen på HiST har flere kvitrere rundt omkring i korridorene. Her er de jeg vet om i farten!

Ivar Sørensen
https://twitter.com/ivarsorensen

Marion G. Stavsøien
https://twitter.com/MarionStavsoien

Harald Morten Iversen
https://twitter.com/haraldmi

Torkel Haugan Hansen
https://twitter.com/torkelhh

Svein Arne Sikko
https://twitter.com/SveinArneSikko

Stian Hårstad
https://twitter.com/avlyd

Calle Dons
https://twitter.com/calledon

Jan Frode Haugseth
https://twitter.com/jafro77

Siri-Malèn Høynes
https://twitter.com/sirimalen

Ruth Grüthers
https://twitter.com/rutgru

Hvem har jeg ikke fått med meg, tro?

Her er flere av dem samlet i ei liste: https://twitter.com/oisteing/lists/tweets-fra-hist

Funnet på nettet sist uke!

Matematisk modell for hipsteres klesvalg (!)
http://mic.com/articles/103172/the-scientific-reason-all-hipsters-look-the-same

Å måle radianer
http://imgur.com/gallery/lJPJsrA

Samling med 12 litt problematiske sammenhenger i matematikk
http://www.businessinsider.com/the-most-controversial-math-problems-2013-3

The random mathematical ponderations of a math geek
http://mathynick.com/

Calculus Rhapsody
https://www.youtube.com/watch?v=uqwC41RDPyg

Litt mer Desmos

Selv om GeoGebra nok er programmet jeg tyr til for alt i geometri og algebra, så har jeg blitt litt misfornøyd med at det som var et program hvem som helst kom i gang med nå blir mer og mer komplekst. Jeg vet mange foretrakk GeoGebra foran TI-nspire nettopp på grunn av dette. Kanskje kan det være greit å se at det fins alternativer, iallfall om det bare skal noe småtteri til. Ei nettside som har høy popularitet i USA er Desmos, og selv om denne sida i bunn og grunn er en graftegner har den noen egenskaper som er verdt å merke seg. Blant annet hvordan man lager glidere for parametre. Se her:

Desmos gir deg et noenlunde standard grafvindu som du kan gjøre vanlige ting med (skalere, flytte osv).

På menyen øverst til venstre kan du legge til ting, f.eks. funksjoner (som du skal tegne grafen til) eller bilder og tekst. Bilder og tekst kan være nyttig om du skal lage grafen PÅ et bilde, for eksempel.

La oss sette inn det vanlige uttrykket for en lineær funksjon. Når vi skriver y=ax+b så ser vi at det dukker opp noen knapper under mens vi skriver:

Det betyr at vi kan lage glidere for disse parametrene bare ved å klikke på knappene det står a og b på. (Eller "all" for å lage glidere for alt på en gang.)

Grafen til funksjonen tegnes med en gang - glidebryterne settes inn automatisk. Så lett er det å lage et interaktivt arbeidsark til å undersøke stigningstall og konstantledd med.
Du kan også klikke på tannhjulet til høyre for å se at du kan velge intervall på gliderne og farge på grafen.

GeoGebra var kjempelett på slike ting før (og er det fortsatt), men lurer på om ikke dette var enda enklere! 

Geobrett

 Du kan lese mer om Picks teorem på f.eks. denne bloggposten: https://reflectionsinthewhy.wordpress.com/tag/geoboards/ 

Et konkretiseringhjelpemiddel vi ofte bruker i matematikk er geobrettet, også kalt pluggbrett. I sin konkrete, fysiske form er dette typisk et kvadrat med spiker i som på bildet (Wikipedia). Vi har plastikkvarianter av disse i bøtter og spann på lærerutdanningen.

Matematikksenteret skriver om Geobrett flere steder. Her kan du finne oppgaver (8 sider pdf) og en idebok (pdf 56 sider) (Sistnevnte er tydeligvis norsk oversettelse av boka Just for Geoboards). Vil du ikke lage brettene selv kan du kjøpe de f.eks. her.

Hva slags oppgaver kan disse brettene brukes til? Vel, det er nok bare fantasien som setter grenser her. Typiske oppgaver er "Hvor mange kvadrater kan du lage på Geobrettet? Det høres jo lett ut, man har et stort kvadrat (hele brettet, sidekanten har da lengde fire, hvis vi setter avstanden mellom spiker til å være 1), seksten små og så er det en liten tellejobb for å finne kvadratene som har sidekant på to og de som har sidekant tre. Men ser vi på bildet øverst så ser vi at det også fins kvadrater som står på skrå. Eller er det kvadrater? Hvordan kan vi finne ut sidelengdene her i så fall? Og hvordan vet vi at det er rett vinkler i hjørnene?

Det er også andre muligheter med todimensjonal geometri. Kan du f.eks. finne et heksagon uten parallelle sider? Kan du finne en likebeint og rettvinklet trekant? Eller en spiss, likebeint trekant?
Symmetrier er at annet tema man kan eksperimentere med. Kan vi lage figurer med en symmetriakse/speilakse? Hva med to akser? Eller tre?
Et naturlig tema er areal av figurer og her fins det mange muligheter. Lag en hvilken som helst figur og finn arealet av den. Kan vi finne arealet på flere måter? Kan du lage figurer med likt areal, men forskjellig lengde på omkretsen? Eller motsatt, lik omkrets og forskjellig areal?

Det er kanskje ikke like naturlig å tenke på brøk som tema på geobrettet. Kanskje kan elevene prøve å illustrere 1/2 eller 3/4 på forskjellige måter? Hva med 3/5?
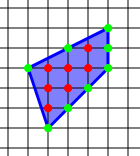Litt mer avanserte muligheter fins også. Et kjent problem/resultat er Picks teorem. Hvis vi lager et polygon på geobrettet så vil noen spiker være hjørner, mens det kan være andre spiker både inni figuren og på kanten av figuren. Vi kan da bruke formelen til Pick til å regne ut arealet av figuren når vi vet antall spiker inni figuren (i) og antall spiker langs kanten (og i hjørnene) av figuren (b), Da blir arealet \( A=i+\frac{b}{2}-1\). På bildet (fra wikipedia) har vi 7 punkter inni og 8 på randen, så arealet blir \(A=7+\frac{8}{2}-1=10\).


Det kan også være greit å ha en interaktiv variant av geobrettet, til bruk på SMARTboard eller nettbrett. Den interaktive varianten av geobrettet, som du så på bloggen til Reflections in the why, kan du finne på
http://www.mathlearningcenter.org/web-apps/geoboard/

Funnet på nettet siste uke

Hva kan du bli når du studerer realfag, da tru?
http://hvakanjegblimedrealfag.no/

Leter man på nettet etter algoritmer kan man finne en hel skokk av morsomme, nyttige og unyttige algoritmer. De fleste av dem klarer vi å gjennomskue slik at vi kan fastslå om de virker hver gang eller ikke. Felles for mange er at de er effektive i gitte situasjoner og dårlige andre ganger. Men siden det er tungvint å huske hvilke situasjoner den og den algoritmen passer best i, så har vi holdt oss til å lære få algoritmer - som fungerer så bra som mulig. I senere tid har fokuset vært mer på å unngå algoritmene, men fokusere på forståelsen bak. Det er greit å kunne noen algoritmer for å håndtere hverdagssituasjoner, men i realiteten har vel disse standardalgoritmene hatt et mye større fokus enn hva som er nødvendig. Her er en algoritme som du kan bruke når du skal undersøke subtraksjon sammen med elevene dine.
http://matematikksenteret.no/content/4594/Kan-du-forklare-denne-nydelige-subtraksjonsalgoritmen

En ny type matematisk legeme er visstnok funnet? Igjen?
http://www.iflscience.com/editors-blog/after-400-years-mathematicians-find-new-class-solid-shapes

Er matematikk oppdaget eller oppfunnet? (Ja, som om vi kan svare på det...)
http://ed.ted.com/lessons/is-math-discovered-or-invented-jeff-dekofsky

Ti prinsipper for multimedialæring:
http://ericsnewblog.blogspot.no/

Fra Better explained finner vi en, om ikke ny så iallfall annerledes, forklaring av definisjonen av sinus.
http://betterexplained.com/articles/law-of-sines/

Litt om Abel dukket opp på plusmath
http://plus.maths.org/content/stubborn-equations

Litt depressiv fysikk
http://thedoghousediaries.com/5916