Gammelt nytt

(Fra The Daily Telegraph, 3. jan. 2001)

Usikker på hvordan denne avisreportasjen skal lenkes til uten å krenke rettighetsinnehavere, men tar sjansen denne gangen. Denne artikkelen stod altså i The Daily Telegraph i 2001. Ti år senere, har noe endret seg? I såfall, hva da?

LaTeX-formler

Har lenge brukt denne oppskriften for å legge inn formler på bloggen: http://watchmath.com/vlog/?p=438

Av en eller annen grunn får jeg ikke dette til å virke lenger, men fant en helt lik kompilator som tolker vanlig LaTeX-kode for deg. Du finner instrukser her: http://mathcache.appspot.com/static/docs.html

Bok: Det tapte symbol (spoilers?)

Etter å ha lest Dan Browns DaVinci-koden (DVK), var forventningene ganske store til oppfølgeren, Det tapte symbol. I DVK følger vi Robert Langdon (på film i ikke helt ukjente Tom Hanks' skikkelse) og hans jakt på den hellige gral, løsninger av koder og mysterier og hesblesende jakter gjennom museer, kunstutstillinger og tempelriddermyter. Som matematiker kan man jo verdsette enhver bok som befatter seg med Det gylne snitt, Fibonaccitall og pentagrammer. Filmen er ikke så verst den heller. Pussig nok har ei tidligere utgitt norsk bok, Sirkelens Ende av Tom Egeland, omhandlet omtrent det samme, også der med en albino i hovedrollen! DVK fulgtes av en mengde filmer og bøker som skulle finne sannheten om DaVinci, tempelridderne, det siste måltid, den hellige gral, Maria Magdalena og alt det der.
Min mening om DVK er at innholdet selvsagt er svært interessant, både som ateist og matematiker, men at den ikke akkurat er skrevet så veldig spennende. Stilen til Dan Brown er å kaste inn hundrevis av kapitler og avslutte alle av dem med en irriterende cliffhanger-klisje.
(Les mer om matematikken i DVK her: http://www.nd.edu/~hahn/pdf%20files/Ch3-MathDaVinci.pdf )
Etter å ha lest DVK leste jeg også de andre bøkene fra Dan Brown, det vil si Digital Fortress (forferdelige greier), Angels & Demons (ganske spennende, har også blitt film) og Iskaldt bedrag (også ganske kjedsom, tror den heter Deception Point på engelsk).
Nok om det, nå har jeg altså omsider fått lest Det tapte symbol, Browns foreløpig siste bok. Også her følger vi Robert Langdon og hans kamp mot ukjente symboler og koder. Jeg skal ikke gå inn på handlingen i boka, den følger stort sett samme mal som de andre bøkene hans. Men også her er det innslag av matematikk. På et tidspunkt involveres Albrecht Dürers Melancholia I, et bilde det er verdt å merke seg av flere grunner.

(Bilde fra Wikipedia)

Her er det flere matematikkobjekter å merke seg. Kula, polyederet og måleinstrumenter. Men det viktigste for handlingen i Det tapte symbol er det magiske kvadratet oppe til høyre. Som du ser er summen av hver rad eller kolonne 34. I tillegg er summen på en diagonal 34. Det gjelder også summen av hjørnetallene. En ekstra bonus Albrecht Dürer har fått til er at summen i hvert 2x2-kvadrat også er 34, også for 2x2-kvadratet i midten.

Les mer om Dürers kunst og matematikk her og her.

Bok: A mathematician's lament

Omsider fikk jeg lest A Mathematician's Lament av Paul Lockheart. For en god stund siden leste jeg PDF-fila som er en slags miniatyrutgave av denne boka. Den har sirkulert på Internett ganske lenge, og har vært mye lest og diskutert i matematikkmiljøer. Hvis du ikke har lest den enda anbefaler jeg sterkt at du setter av noen minutter til det. Du kommer til å være takknemlig etterpå (for det bør du være). Denne posten dreier seg imidlertid om boka som kom i kjølvannet av populariteten til pdf-fila, som egentlig trolig bare var ment som et dokument skrevet i frustrasjon. Boka er heller ikke lang, forsåvidt - den teller bare 140 sider. 

Bilde fra Amazon.com

Boka er for det meste en personlig beretning om hvordan man oppfatter at matematikkundervisning er, og hvordan forfatteren mener læring av matematikk bør skje. Jeg sier vel ikke for mye dersom jeg sier at Lockheart er svært kritisk til hvordan ting skjer nå om dagen. Boka er skrevet i 2009, så den er i høyeste grad aktuell. 

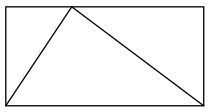
Forfatteren starter med å introdusere oss for hvordan han oppfatter matematikk i skolen ved å beskrive et marerittliknende opplegg i musikkfaget. Elevene tvinges til å lære noter, notesystemer, oppbyggingen av instrumenter, pugge satser og lyttepartitur osv. Uten å i det hele tatt få komponere musikk, skape samspill eller beherske et instrument. Videre tar han for seg et svært enkelt eksempel fra matematikken, med en trekant tegnet inn i et rektangel. En suverent enkel figur, med et enkelt spørsmål "Mon tro hvor stor del av rektangelet trekanten opptar?". Så enkelt at hvem som helst kan begynne å undersøke det, og veldig mange vil finne gode svar - samt nye spørsmål. Da er vi i gang! :) En slik figur kan passe godt i for eksempel ungdomsskolen også, dersom man ønsker å sette fokus på hvordan man kan forstå formelen for arealet av en trekant. 

Her kan du også gå inn på http://mattegreier.blogspot.com/2009/10/areal-og-omkrets.html og se hvordan man kan bruke GeoGebra til å vise at hvor toppunktet på en trekant plasseres hen i et slikt tilfelle, ikke har betydning for arealet.) Håpet er at en slik figur kan få eleven til å ytre ordene "Men hva hvis..."

Figur fra republicofmath.com

Jeg synes det er en veldig frisk måte å skrive på, når forfatteren velger å bruke Simplicio og Salviati-teknikken. Ukjente navn for meg, selv om det å bruke dialog vel må sies å være godt kjent. 

På wikipedia finner vi følgende forklaring angående boka til Galileo Galilei, Dialogue Concerning the Two Chief World Systems :

• Salviati argues for the Copernican position and presents some of Galileo’s views directly, calling him the “Academician” in honor of Galileo’s membership in the Accademia dei Lincei. He is named after Galileo’s friend Filippo Salviati (1582–1614).

• Sagredo is an intelligent layman who is initially neutral. He is named after Galileo’s friend Giovanni Francesco Sagredo (1571–1620).

• Simplicio, a dedicated follower of Ptolemy and Aristotle, presents the traditional views and the arguments against the Copernican position. He is supposedly named after Simplicius of Cilicia, a sixth-century commentator on Aristotle, but it was suspected the name was a double entendre, as the Italian for “simple” (as in “simple minded”) is “semplice”.^[7] Simplicio is modeled on two contemporary conservative philosophers, Ludovico delle Colombe (1565-1616?), Galileo’s fiercest detractor, and Cesare Cremonini (1550–1631), a Paduan colleague who had refused to look through the telescope.^[8] Colombe was the leader of a group of Florentine opponents of Galileo’s, which some of the latter’s friends referred to as “the pigeon league”.^[9]

(Sagredo dukker ikke opp i denne boka, da.) Poenget er, Simplicio stiller "de dumme spørsmålene" og har et konservativt syn (i Galileis tilfelle, at jorda er flat og verdensbildet er geosentrisk), mens Salviati kommer med de reflekterte og opplysende svarene (det heliosentriske verdensbilde). Likheten til debatten om konservativ kontra progressiv utdanning er slående. 

Et veldig godt eksempel på hvordan Lockheart argumenterer er løsning av andregradslikninger. Jeg husker vi brukte lang tid på dette på videregående skole, og kanskje var det noen som også forstod hvorfor og hvordan det måtte bli som det måtte bli. Men for de flestes tilfelle handlet dette om å finne en a, b og c og sette inn i abc-formelen (den var så mye brukt at den til og med fikk et eget navn!). Mange ganger. Noen ganger hendte det at læreboka prøvde å lure oss til å tro at dette var nyttig i det virkelige liv, ved å lage en kvasi-reell kontekst som "Hvor lander kanonkula når den skytes ut etter en funksjon som er...". Som om vi noengang vet den funksjonen!? Eller har behov for å skyte med kanon, for den saks skyld.  Lockheart hevder at samfunnet sannsynligvis ikke har spesielt god nytte av at befolkningen går rundt med noen vage minner om en abc-formel, en formel vi ikke husker riktig, kanskje aldri forstod, og neppe kan bruke til noe. Så hvorfor bruke så mange timer på å trene oss på å bruke den? Jeg spør som regel førsteklassingene på lærerutdanningene om denne formelen og det er svært få som husker den, selv om det bare har gått måneder siden de gikk videregående skole. 

Et viktig spørsmål dukker alltid opp i slike diskusjoner.

Simplicio: But we don't have time for every student to invent mathematics for themselves! (...)

Ja, det er iallfall sikkert! Men ingen påstår nå heller at elevene skal finne opp matematikken på nytt. Det tok tross alt flere tusen år å komme dit ungdomsskoleelevene befinner seg i dag, matematisk sett. Det fins mange forskere som mener at all matematikk KAN læres, og læres svært godt, ved å introdusere elevene for situasjoner og fenomener de selv kan studere og trekke hypoteser og slutninger ut av. Og de har sikkert rett. Men det de mener er jo at vi ikke kan gjøre dette innenfor tidsrammene og den mengden ting vi skal gjennom slik det er i dag. Men det er klart, hvis man halverer den tiden man bruker på øve på oppgaver man ikke har bruk for... kanskje ikke all matematikk er helt nødvendig å bruke tid på i skolen heller. Jeg tror ikke mange av elevene som ikke skal studere matematikk har bruk for andregradslikningen og formler for å løse den. Jeg kan ikke en gang finne på et eneste eksempel fra mitt daglige liv der jeg har bruk for noe så enkelt som arealet av en trekant eller pytagorassetningen. Og DEN var iallfall livsviktig å kunne, fikk vi høre av lærerene våre. Da jeg selv var lærer første gang befant jeg meg plutselig foran en klasse som skulle lære om trekantarealet. Det alltid like aktuelle spørsmålet "hva skal dette brukes til" dukket selvsagt opp. (Pussig nok, hvorfor er det bare matematikk som må forsvare seg med å være brukbart til noe? Kan vi ikke få være like unyttige som diktanalyse og kunnskap om fotosyntese!? Da kan det jo til og med bli oppfattet som gøy!) Jeg følte jo jeg måtte svare eleven, og kom med et eksempel om at man kunne jo få god bruk for dette om man på et tidspunkt skulle så plenfrø på en trekantet plen og måtte vite hvor stort arealet er! (Du trenger ikke lete lenge i skolebøker for å finne tilsvarende idiotiske oppgaver). For:

1. Hvem i all verden har trekantete hager?

2. Hvem regner ut arealet av plena si med formler når man uansett må gå ut og ta mål - og da kan man jo like gjerne måle plena.

3. Hvor mye motivasjon er det for eleven hvis dette er det beste eksemplet jeg kommer på? At man KANSKJE skal ha en HAGE en gang!?!? Ikke halvparten av de jeg kjenner har plen i det hele tatt! 

Bilde fra
http://ejad.best.vwh.net/java/pythagoras/history.html

Og hva med pytagorassetningen, den er da vel viktig, den brukte vi tross alt på løkka for å lage hjørnet der cornerflagget skulle stå.  Vel, nei, det kan jeg ikke huske noen gjorde. Ikke blir det nøyaktig likevel, og er det ikke noe stort poeng å få nittigraderen helt nøyaktig kan man like gjerne bruke øyamål. Men i prinsippet kan man lage tolv knuter på et tau og legge tauet i en trekant slik at det blir henholdsvis tre, fire og fem knuter i hver side. Da får vi en nittigradersvinkel. .... tja... dersom man har nøyaktig avstand mellom knutene... altså i PRINSIPPET går det fint, og prinsippet må man gjerne bruke mye tid på. La ungene finne ut av dette, gi de gjerne tau både med og uten knuter. Men ikke si at vi lærer dette fordi det er så veldig nyttig!

Hvem i all verden var det jeg lurte med disse oppkonstruerte liksom-realitetene? Mest meg selv. Og alle elevene. 

Uansett - LES denne boka, den er så veldig verdt det, og bør få et publikum langt utenfor skolestua. Du vil ha nytte av det (der sa jeg det igjen). De eventuelle elevene dine vil ha nytte av det. Kanskje forandrer du ikke verden i dag, kanskje ikke i morra, kanskje endrer du bare deg selv bittelitt. Og så kanskje litt til. Til slutt er det kanskje en elev som sitter igjen med et litt annet inntrykk av matematikken enn det han ellers ville ha gjort. Og klarer vi det er det heller ikke så aller verst.

Andre har også skrevet om denne boka:

Squarecircles: http://www.squarecirclez.com/blog/a-mathematicians-lament-how-math-is-being-taught-all-wrong/2828

maa.org: http://www.maa.org/devlin/devlin_03_08.html

(written by Keith Devlin, who also wrote the foreword to the book).

Så sent som i dag var det et debattinnlegg om Dagens dannelse i dagbladet, der artikkelforfatteren kanskje kunne hatt nytte av å lese boka til Lockheart:

http://www.dagbladet.no/2011/07/05/kultur/skole/utdanning/skolepolitikk/17192843/

Undervisningspraksis

Hvorfor tror vi i lærerutdanningen at vi kan endre andres praksis, når vi ikke klarer å endre vår egen?